Chapter 8
Similarity
Some Properties of Proportions
- The Means-extremes Product Property:
If ab=cd, then ad=bc
where a,d are extremes and b,c are means.
If ab=cd, then b is called the geometric mean of a and c. - Invertendo Property:
If ab=cd then ba=dc - Alternando Property:
If ab=cd, then ac=bd (or db=ca) - Componendo Property:
If ab=cd, then a+bb=c+dd - Dividendo Property:
If ab=cd, then a−bb=c−dd - Componendo and Dividendo Property:
If ab=cd, then a+ba−b=c+dc−d - corresponding angles must be equal, and
- corresponding sides must be proportional.
- လိုက်ဖက်ထောင့်များတူညီရမည်။
- လိုက်ဖက်အနားများ၏အလျားများအချိုးတူရမည်။
- State why the two polygons are, or are not similar. In the given figure, find the values of x and y.
- Complete the proportions.
- State whether the proportions are correct for the indicated similar triangles.
- Use the Basic Proportionality Theorem (BPT) and its corollary to complete the proportions for the adjoining figures.
- To find the value of x in the figure, a student wrote the proportions x10=48.
(a) Is this correct?
(b) Another student wrote the proportion xx−4=48.
Is this correct?
(c) Write a simpler proportion that will give the correct answer. - Find the value of x in each of the figure below.(They are not drawn to scales.)
- Given △ PQR with ST∥PQ and lengths of segments are marked. Which of the following proportions are correct?
- If PQ ∥ LM ∥ AB, and the lengths are as shown, how long are the segments MQ and BM?
- If the segments in the figure have the lengths indicated, is UV ∥ RT? Justify your answer.
- Given the figure as marked with ST ∥ PQ, find the lengths of the segments PS, SR, RT and TQ.
- Use the given information to tell whether each pair of triangles is similar or not. Give a reason for each answer.
- In each of the following triangles, the lengths of certain segments are marked. Find the values of x, y, z, w and v.
- Find the marked lengths in each of the figures.
- In the figure, XY ∥ PR and VT ∥ QR. If PTTR=32, QYYR=21 and PQ=15cm, calcaulate
(a) the lengths of PV, PX and XV.
(b) the numerical vaalues of YWWX and VWQY.
- Which of the following proportions follow from the fact that AE bisects ∠ WAV in △ WAV?
- AX bisects ∠ CAB. Complete the following statements:
(a) A C : A B =-----
(b) A B : A C =-----
(c) X C : X B =----- - PT bisects ∠ RPS. Complete the following statements:
(a) P Q : P R =-----
(b) T R : P R =-----
(c) Q R : T R =----- - What can you say about the rays AD, BE and CF?
- If AD and AE are bisectors of the interior and exterior angles at A of ABC, then which of the following are true?
- Find the value of x in each of the following figures.
- Find the unknown marked lengths in the figure.
- AB= 12cm, BC= 9cm, CA= 7cm.
BD bisects B and AG= AD, CH= CD.
Calculate BG, BH. Does GH ∥ AC? - In ABC, DE ∥ BC, AD=2.7cm. DB=1.8cm and BC=3cm.
Prove that BE bisects ∠ ABC. - In a parallelogram ABCD, AB= 3.6 cm, BC= 2.7 cm. AX= 3.2 cm, XC= 2.4 cm. Prove that △ BCY is isosceles.
- Calculate BD and DC in terms of a, b, c.
- In the figure ∠ PQR= 90°, QS ⊥ PR. Complete each of the following true statements.
(a) △ PQR ∼ △? ∼ △?
(b) QS is the geometric mean between ? and ?
(c) QR is the geometric mean between ? and ?
(d) ?PQ=PQ? - In the figure CD ⊥ AB and C=90°. If DE ⊥ BC, DF ⊥ CA, write out all the triangles that are similar to △ABC.
- Find the length of each marked segment.
- In the figure, if AD= 10 cm, AB= 8 cm, BC= 4 cm, find the length of CD.
- In the figure, find the distance of D from A.
- A parallelogram with sides 8 cm and 15 cm has a diagonal of 17 cm. Is it a rectangle?
- In the figure, △ ABC, △ ACD, △ ADE are right triangles and AB= BC= CD= DE. Show that AE= 2 AB.
8.1 Ideas of Similarities and Similar Triangles
Geometric figures that are of the same shape but not necessarily of the same size are said to be similar figures.ပုံသဏ္ဌာန်ဆင်တူပြီးအရွယ်တူရန်မလိုသော geometry ပုံများကိုသဏ္ဌာန်တူပုံများဟုခေါ်သည်။
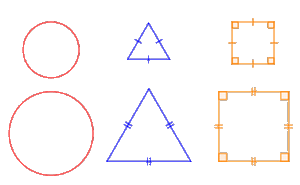
The conditions for two polygons to be similar are
Definition
Two triangles whose corresponding angles are equal and whose corresponding sides are proportional are said to be similar.လိုက်ဖက်ထောင့်များတူညီပြီးလိုက်ဖက်အနားများအချိုးတူသောတြိဂံနှစ်ခုသည်သဏ္ဌာန်တူကြသည်။
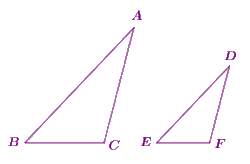
8.2 The Basic Proportionality Theorem
Postulate 1
If three parallel lines intersect two transversals, then the lines divide the transversals proportionally.မျဉ်းပြိုင်သုံးကြောင်းသည်ဖြတ်မျဉ်းနှစ်ကြောင်းကိုပိုင်းဖြတ်လျှင်ထိုမျဉ်းများသည်ဖြတ်မျဉ်းများကိုအချိုးတူစွာပိုင်းဖြတ်ကြ၏။
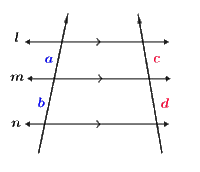
if l∥m∥n, then ab=cd.
8.3 Basic Theorems on Similar Triangles
8.4 The Angle Bisector Theorem
If B is a point on the line containing segment AC, then ABBC is the ratio in which B divides AC.B သည် မျဉ်းပြတ် AC ပေါ်ရှိအမှတ်တစ်ခုဖြစ်လျှင်အချိုး ABBC ဆိုသည်မှာ B က AC ကိုပိုင်းဖြတ်သောအချိုးပင်ဖြစ်သည်။
(i)
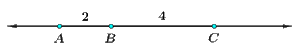
ABBC=24=12
B divides AC internally in the ratio 1 ∶ 2.
B က AC ကို 1 ∶ 2 ဖြင့်အတွင်းပိုင်းပိုင်းဖြတ်သည်။
(ii)
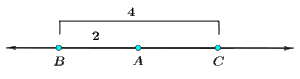
ABBC=24=12
B divides AC externally in the ratio 1 ∶ 2.
B က AC ကို 1 ∶ 2 ဖြင့်အပြင်ပိုင်းပိုင်းဖြတ်သည်။
8.5 The Pythagoras Theorem
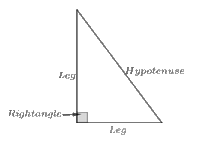
A triangle with a right angle is called a right triangle and the sides which determine the right angle are called legs of the right triangle, and the side opposite the right angle is called the hypotenuse.ထောင့်မှန်တစ်ခုပါသောတြိဂံကိုထောင့်မှန်တြိဂံဟုခေါ်သည်။ထောင့်မတ်ကျနေသောအနားများကိုထောင့်မှန်ဆောင်အနားများဟုခေါ်ပြီးထောင့်မှန်နှင့်မျက်နှာချင်းဆိုင်သောအနားကိုထောင့်မှန်ခံအနားဟုခေါ်သည်။
Geometric Mean (GM)
If ba=cd ie b2=ac then b is called the geometric mean between a and c.Converse of Pythagoras Theorem
If a triangle has sides with lengths a, b, c and a2+b2=c2, then the triangle is a right triangle.တြိဂံတစ်ခု၏အနားများ၏အလျားများသည် a, b, c ဖြစ်ကြပြီး a2+b2=c2 ဖြစ်လျှင်ယင်းတြိဂံသည်ထောင့်မှန်တြိဂံတစ်ခုဖြစ်၏။
∠ ACB=90° ဖြစ်၏။
8.6 Special Right Triangles
There are two special types of right triangles.ထောင့်မှန်တြိဂံအထူးပုံစံနှစ်ခုရှိသည်။
(i)
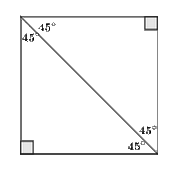
The isosceles right triangle (45°- 45° right triangle):A triangle is formed by two sides and a diagonal of a square.
စတုရန်းတစ်ခုတွင်ထောင့်ဖြတ်မျဉ်းတစ်ကြောင်းဆွဲခြင်းဖြင့်နှစ်နားညီအထူးထောင့်မှန်တြိဂံတစ်ခုရရှိသည်။
(ii)
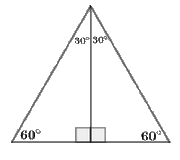
(30°- 60° right triangle):An altitude of an equilateral triangle determine the right triangle with acute angles of measures 30° and 60°.
30° နှင့် 60° ရှိသောထောင့်ကျဉ်းနှစ်ခုနှင့်သုံးနားညီတြိဂံ၏အမြင့်မျဉ်းဖြင့်ဖွဲ့စည်းထားသောအထူးထောင့်မှန်တြိဂံတစ်ခုဖြစ်သည်။
Problems
Example 1
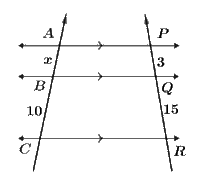
In the following figure if AP ∥ BQ ∥ CR, find the value of x.Example 2
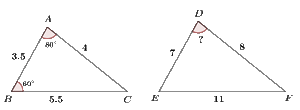
Determine whether the following pairs of triangle are similar or not. If they are similar, state why.Example 3
Find the value of angle D.Exercise (8.1)
4. Given :△PQR∼△UVW and lengths of sides are as marked . Find : The values of x and y .
5.The measures of two angles of △ XYZ are 82° and 16°. Find the measures of the angles of a triangle similar to △ XYZ.
Exercise (8.2)
8. Given :ADDB=21 Prove :AXXB=31
9. Given :AE=EB,BDDC=23 Find : The ratio CHCE
.png)
Exercise (8.3)
.png)
5. Given : Parallelogram B I R D : I G bisects ∠ B I R . Prove :BEEI=RGGI
.png)
6. Given :RQ⊥PQ,PQ⊥PT,ST⊥PR. Prove :ST.RQ=PS.PQ
.png)
7. Given : Parallelogram ABCD;PQ∥MB Prove :△ABM∼△CQP.
.png)
8. △ ABC and △ CAD are drawn on opposite sides of AC such that AB : BC : CA= CA : AD : DC.
Prove that DC ∥ AB.
.png)
Exercise (8.4)
.png)
.png)
.png)
.png)
(a) ∠ D A E = 90°
(b) B D : D C =B C : C E
(c) B D : D C =B E : C E
(d) A D : A E =D C : C E
.png)
.png)
.png)
.png)
.png)
.png)
12. Given :AH bisects ∠BAC in △ABC.EH∥AC. Prove :BEEA=BAAC
.png)
13. Given : In △ABC,BM=MC;MX bisects ∠AMBMY bisects ∠AMC. Prove :XY‖BC.
.png)
14. Given : In △ABC,∠A=2∠C;AD bisects ∠BACDE bisects ∠ADB. Prove :BEEA=BAAC.
.png)
Exercise (8.5)
.png)
.png)
.png)
.png)
.png)
8. Given :AD⊥BC Prove :AB²−AC²=BD²−DC²
.png)
9. Given :∠BAC=90°,D is any point on AB. Prove :BC²+AD²=AB²+CD²
.png)
10. Given :∠QPR=90°,PS⊥QR. Prove :1PS2=1PQ2+1PR2
.png)
11. Given :AD⊥BC,AD=9 cm,BD=13.5 cm,DC=6 cm. Prove :∠BAC=90°
.png)

.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
.png)
إرسال تعليق